Verhoudingen deel I: Introductie: Difference between revisions
| Line 84: | Line 84: | ||
== 17de-eeuwse mathematische uitgangspunten van Nederlandse architectuur == | == 17de-eeuwse mathematische uitgangspunten van Nederlandse architectuur == | ||
[[File:Schielandshuis.jpg|thumb| | [[File:Schielandshuis.jpg|thumb|238x238px|Schielandshuis]] | ||
Wanneer men op zoek gaat naar 17de-eeuwse ontwerpmethoden die in Nederland werden gehanteerd, is het van belang in acht te houden dat het vinden van mooie mathematische figuren in het ontwerp niet het doel is. Een mathematisch schema moet vooral zinvol zijn bij het bepalen van de definitieve afmetingen van een gebouw. Omgekeerd moet een achteraf gemaakt ontwerpmethode een 'sleutel' bieden voor de ordening van het gebouw: cruciale punten van het systeem moeten dan samenvallen met de hoofdlijnen van het ontwerp. Op deze wijze kan onderscheiden worden wat zin en onzin is van proportieschema's. De ontwerpmethoden zijn te achterhalen door de ontwerpen nauwkeurig na te meten. De originele tekeningen moeten hiervoor gebruikt worden, géén foto's of losse schetsen. | Wanneer men op zoek gaat naar 17de-eeuwse ontwerpmethoden die in Nederland werden gehanteerd, is het van belang in acht te houden dat het vinden van mooie mathematische figuren in het ontwerp niet het doel is. Een mathematisch schema moet vooral zinvol zijn bij het bepalen van de definitieve afmetingen van een gebouw. Omgekeerd moet een achteraf gemaakt ontwerpmethode een 'sleutel' bieden voor de ordening van het gebouw: cruciale punten van het systeem moeten dan samenvallen met de hoofdlijnen van het ontwerp. Op deze wijze kan onderscheiden worden wat zin en onzin is van proportieschema's. De ontwerpmethoden zijn te achterhalen door de ontwerpen nauwkeurig na te meten. De originele tekeningen moeten hiervoor gebruikt worden, géén foto's of losse schetsen. | ||
Het gevoel van mooie maatverhoudingen was in de 17de-eeuwse Nederlandse cultuur diep geworteld. Ambachtslieden, die zich niet bewust waren van de zogezegd humanistische opvatting over proporties, konden zelfs eenvoudiger werken middels deze maatverhoudingen. | Het gevoel van mooie maatverhoudingen was in de 17de-eeuwse Nederlandse cultuur diep geworteld. Ambachtslieden, die zich niet bewust waren van de zogezegd humanistische opvatting over proporties, konden zelfs eenvoudiger werken middels deze maatverhoudingen. | ||
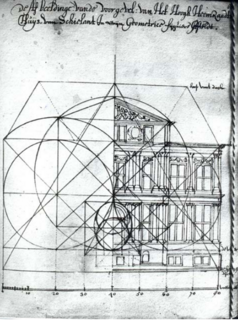
Een duidelijke bron voor een Nederlands 17de-eeuws ontwerpproces is uiteraard met aanwijzingen van de architect zelf. Op deze manier kan men onderzoeken zonder het risico van 'overinterpretatie'. Zo ontwierp Jacob Lois in 1662 het Schielandshuis in Rotterdam waar een proportieschema van bewaard is. De analyse van dit gebouw is onderdeel geweest van een [https://www.researchgate.net/publication/307673231_Proportional_Design_Systems_in_Seventeenth-Century_Holland onderzoek.] | Een duidelijke bron voor een Nederlands 17de-eeuws ontwerpproces is uiteraard met aanwijzingen van de architect zelf. Op deze manier kan men onderzoeken zonder het risico van 'overinterpretatie'. Zo ontwierp Jacob Lois in 1662 het Schielandshuis in Rotterdam waar een proportieschema van bewaard is. De analyse van dit gebouw is onderdeel geweest van een [https://www.researchgate.net/publication/307673231_Proportional_Design_Systems_in_Seventeenth-Century_Holland onderzoek.] | ||
[[File:Ontwerpsysteem Schielandhuis (1662), Jacob Lois.png|thumb| | [[File:Ontwerpsysteem Schielandhuis (1662), Jacob Lois.png|thumb|321x321px|Ontwerpsysteem Schielandshuis (1662), Jacob Lois]] | ||
=== Het Schielandshuis van Jacob Lois === | === Het Schielandshuis van Jacob Lois === | ||
Revision as of 09:32, 3 May 2023
https://www.dbnl.org/tekst/_zev001199101_01/_zev001199101_01_0004.php
De oorsprong van de Westerse proportiesystemen
Egypte en Babylon
3000 v.Chr.
Hier vinden we de eerste voorbeelden van een strikt mathematische ordening. Hoe is het verschijnsel te verklaren dat kunstenaars en architecten geometrische piramiden, tempels en grafkamers bouwden? Zij waren ongetwijfeld gebonden aan zorgvuldig uitgewerkte regels en voorschriften, die ze niet mochten en niet wilden breken. In deze tijd was het intellectuele leiderschap in handen van een priesterkaste. Zij waren het die de rituelen en ceremonies leidden, en de gebouwen moesten voldoen aan de regels die zij vaststelden. Omdat alle grote kunst van die tijd sacrale kunst was, weerspiegelde ze de kosmische orde die door priesters werd geduid en bewaakt.
De Grieken
750 v.Chr. - 500 na Chr.
In de opkomende beschavingen van de Griekse stadstaten, met name die van Athene, treffen we een nieuwe klasse van vrije burgers aan. Zij waren door middel van rationeel onderzoek het universum aan het doorgronden - het waren de Grieken die de wiskunde uitbouwden tot een theoretische wetenschap en die de eerste pogingen deden de natuur langs mathematische wegen te verklaren. Dit maakte het ontstaan van de westerse beschaving mogelijk.
Pythagoras
Rond 550 v.Chr. had Pythagoras de meetkunde uitgebouwd tot een theoretische wetenschap. Waarschijnlijk heeft Pythagoras in aansluiting op Egyptische tradities zijn theoretische bevindingen toegepast op natuurlijke verschijnselen waarbij hij zeer bijzondere verhoudingen en een vrije regelmaat ontdekte. Zijn waarnemingen brachten hem tot de overtuiging dat bepaalde verhoudingen en proporties de absolute waarheid met betrekking tot de harmonische opbouw van de wereld belichaamden. Zijn observatie dat muzikale samenklanken berusten op vaste en onveranderlijke verhoudingen van de snaren van een muziekinstrument bevestigde hem in deze overtuiging.
Plato
In het voetspoor van Pythagoras ondernam Plato een poging de ordening van de wereld - een volkomen mathematische wereld - te verklaren. Hij legde dit vast in Timaeus, en dit laat nog steeds zijn invloed gelden. Alle Europese proportiestelsels bouwden in meerdere of mindere mate voort op de pythagoreïsch-platonische traditie en Timaeus werd veel bestudeerd. De kern van de bleef behouden in alle belangrijke middeleeuwse en renaissance handboeken. Plato stelde zich in Timaeus voor dat alle materie is opgebouwd uit vijf regelmatige lichamen, er zijn namelijk niet meer dan vijf ruimtelijke vormen mogelijk met gelijke zijden, gelijke vlakken en gelijke hoeken. Hij verbindt deze ruimtelijke vormen ook met één van de vier elementen. Hij kende aan al deze vormen een diepe, zelfs mystieke betekenis toe.
| Ruimtelijke vorm | Element | Samenstelling | |
| Viervlak | Tetraëder | Vuur | Gelijkzijdige driehoeken |
| Kubus | Hexaëder | Aarde | Vierkanten: diagonaal driehoek |
| Achtvlak | Octoëder | Lucht | Gelijkzijdige driehoeken |
| Twaalfvlak | Dodecaëder | Luchtruim | Vijfhoeken opgebouwd uit gelijkbenige driehoeken |
| Twintigvlak | Isosaëder | Water | Gelijkzijdige driehoeken |
Euclides
250 jaar na Pythagoras heeft Euclides het werk van Pythagoras samengevat en gesystematiseerd. Wat Euclides aanduidde als 'een lijn snijden in haar uiterste en middelste delen', en wat Plato voor hem eenvoudigweg aanduidde als de 'snede', is wat wij tegenwoordig de gulden snede noemen.
De Middeleeuwen
500 - 1500
In de geschiedenis van de Europese kunst zijn er twee proportiestelsels gehanteerd:
- Gehele getallen en eenvoudige breuken;
- Elementaire geometrische figuren.
In de Middeleeuwen verkoos met het tweede, geometrische type. Er kan dus gezegd worden dat de gelijkzijdige driehoek, het vierkant en de vijfhoek hoekstenen de middeleeuwse esthetiek vormden. Al mogen we aannemen dat de middeleeuwse bouwers zich hoogstwaarschijnlijk niet bewust waren van de kosmische lading die de Timaeus eraan toedichtte, toch konden zij zich van hun werk geen voorstelling maken die los stond van een van deze elementaire geometrische vormen. De Renaissance wordt gekenmerkt door de voorkeur voor het eerste, rekenkundige proportiemodel.
De tijdsgeest van de Middeleeuwen
Kunstenaars van het de Middeleeuwen hechtten zo'n groot belang aan de geometrische vormen dat zij ze geen moment uit het oog verloren, zelfs niet als zij een gebruiksvoorwerp ontwierpen. De middeleeuwse kunstenaar probeert een vooraf bepaalde geometrische norm te projecteren op zijn beeldentaal. Robert Grosseteste, Middeleeuwse Engelse staatsman, filosoof, theoloog en bisschop, stelde: 'Het is onmogelijk de natuur te kennen zonder geometrie. De principes van de geometrie hebben absolute geldigheid in heel het universum en voor elk van de delen daarvan. Lijnen, hoeken en geometrische figuren zijn het, waarmee we alle natuurlijke verschijnselen moeten verklaren.'.
We kunnen deze stelling nog aanvullen met de middeleeuwse conceptie van de relatie tussen de vooraf bepaalde vorm en de voorstelling die de mens zich daarvan maakt: 'De vorm (en we mogen dat nu vertalen als: de vooraf bepaalde geometrische vorm) is het voorbeeld dat de kunstenaar voor de geest staat (forma est exemplat quod respicit artifex) en de navolging van dit voorbeeld stelt hem in staat een gelijkend werk te maken (ut ad eius imitionem et similitudinem formet suum artificium).'.
De Dom van Milaan
Tijdens een bijeenkomst in 1391 werd besloten dat het centrale thema de vraag zou zijn of de kerk zou moeten verrijzen volgens het vierkant of het driehoek. Het besluit was dat ze tot de driehoekige figuur zou moeten verrijzen en niet hoger. Slechts een jaar later werd dit besluit al herroepen en maakte men een nieuw plan gebaseerd op een raster van vierkanten. Maar, inmiddels was de bouw al begonnen op basis van het eerdere besluit. De hoogte van het gebouw leek namelijk te groot te worden, waardoor men besloot om over te schakelen op een ander geometrisch patroon. Opmerkelijk is, is dat er niet voor gekozen werd om eenvoudigweg het gebouw minder hoog uit te laten voeren, maar dat dit alleen gedaan kon worden op grond van een bestaande geometrische conceptie. Deze conceptie vond men in de Pythagoreïsche driehoek.
De Renaissance
1430 - 1630
De kunstenaar van de Renaissance probeert een metrische norm te ontlenen aan de natuurlijke verschijnselen die hem omgeven. Deze metrische norm wordt vastgelegd in getalsmatige verhoudingen, en het doorvoeren ervan is alleen mogelijk als de verhouding van elk onderdeel tot het geheel is gerelateerd aan een gemeenschappelijke maateenheid. Om in een figuur, een schilderij of een gebouw een samenhangend stelsel van numerieke verhoudingen te kunnen doorvoeren moest een speciale meetmethode worden ontwikkeld, en de maateenheid moest van geval tot geval kunnen worden aangepast.
De tijdsgeest van de Renaissance
Het Renaissance-denken was (o.a.) gericht een verzoening tot stand te brengen tussen Plato en het christendom. Men probeerde de universele harmonie van Gods schepping te interpreteren in termen van de platonische getallenleer. De kunstenaars geloofden dat deze universele harmonie in hun werk tot uitdrukking moest komen. Ontbrak deze, dan was het resultaat een verstoring van de harmonie der sferen. Renaissance-kunstenaars en -architecten geloofden in een allesomvattende (muzikale) harmonie volgens pythagoreïsch-platonische traditie.
Rekenkundige porporties
Belichaamd in de verhoudingen van de Griekse toonladder, worden rekenkundige proporties uitgedrukt in gehele getallen of eenvoudige breuken. Daarentegen kunnen veel van de proporties die zijn gebaseerd op de geometrie van de Timaeus niet in gehele getallen of eenvoudige breuken worden uitgedrukt. R. Wittkower stelt dat commensurabiliteit te beschouwen is als het kernbegrip van de renaissance-kunst. Gehele getallen en eenvoudige breuken worden door hem 'commensurabele' verhoudingen genoemd, en de geometrie van de Timaeus 'incommensurabel'. De irrationele proporties hebben de Renaissance-kunstenaars voor onoplosbare problemen gesteld, want de Renaissancistische benadering van de proportie werd bepaald door een nieuwe organisch-mathematische benadering van de natuur, waarin alle verhoudingen een numeriek (aritmische en niet geometrisch) karakter hadden. Alberti stelt: 'Meten is een betrouwbare en ondubbelzinnige (want commensurabele) notatie van afmetingen, die evenveel inzicht verschaft in de onderlinge verhoudingen van de afzonderlijke delen, als in de verhouding van elk deel tot het geheel.'.
Het menselijke figuur
Als het gaat om het menselijke figuur, waaraan Leonardo Da Vinci veel studies wijdde, is een systeem van vaste metrische verhoudingen tussen de afzonderlijke lichaamsdelen en tussen elk deel en het geheel alleen mogelijk door een maateenheid te postuleren. De grootste kunstenaars van de vijftiende en zestiende eeuw waren eindeloos bezig met het uitwerken van deze metrische verhoudingen. Deze inspanningen waren niet alleen van theoretisch belang, ze waren ook van groot belang voor de praktijk. Men ging zover dat de maten van de modellen werden aangepast aan de ideale verhoudingen, zoals bij het portret van Karel V door Titiaan. Voor ideale proporties ging met ook te rade bij klassieke beelden. Classicistisch georiënteerde kunstenaars gaven hun modellen de proporties van deze voorbeelden en lieten ze zelfs dezelfde poses aannemen. Ruim 4 eeuwen later kwam Le Corbusier met de Modulor-schaal.
Leonardo da Vinci
Muzikale harmonie en architectuur
Dezelfde werkwijze werd ook gevolgd op het gebied van architectuur. Hierbij wordt meestal dan ook gebruik gemaakt van de voorschriften van Vitruvius. Een zeer strikte toepassing van getalsmatige verhoudingen vind je bij de werken van Palladio. Neem de plattegrond van Villa Thiene, de vertrekken zijn gebaseerd op de reeks 12:18:36. Alberti noteerde, verwijzend naar Pythagoras: 'De getallen waarop de ramenklanken zijn gebaseerd die onze oren strelen, zijn dezelfde die ons oog en onze geeft behagen.'. Zo zegt Sir Henry Wotton, in wat andere woorden, poëtisch dat ‘symmetrie kan veranderen in symfonie, en een harmonie voor het oor in een harmonie voor het oog’. Alberti presenteert een rekenkundige proportieleer die is afgeleid van de harmonische intervallen van de toonladder.
17de-eeuwse mathematische uitgangspunten van Nederlandse architectuur
Wanneer men op zoek gaat naar 17de-eeuwse ontwerpmethoden die in Nederland werden gehanteerd, is het van belang in acht te houden dat het vinden van mooie mathematische figuren in het ontwerp niet het doel is. Een mathematisch schema moet vooral zinvol zijn bij het bepalen van de definitieve afmetingen van een gebouw. Omgekeerd moet een achteraf gemaakt ontwerpmethode een 'sleutel' bieden voor de ordening van het gebouw: cruciale punten van het systeem moeten dan samenvallen met de hoofdlijnen van het ontwerp. Op deze wijze kan onderscheiden worden wat zin en onzin is van proportieschema's. De ontwerpmethoden zijn te achterhalen door de ontwerpen nauwkeurig na te meten. De originele tekeningen moeten hiervoor gebruikt worden, géén foto's of losse schetsen. Het gevoel van mooie maatverhoudingen was in de 17de-eeuwse Nederlandse cultuur diep geworteld. Ambachtslieden, die zich niet bewust waren van de zogezegd humanistische opvatting over proporties, konden zelfs eenvoudiger werken middels deze maatverhoudingen.
Een duidelijke bron voor een Nederlands 17de-eeuws ontwerpproces is uiteraard met aanwijzingen van de architect zelf. Op deze manier kan men onderzoeken zonder het risico van 'overinterpretatie'. Zo ontwierp Jacob Lois in 1662 het Schielandshuis in Rotterdam waar een proportieschema van bewaard is. De analyse van dit gebouw is onderdeel geweest van een onderzoek.
Het Schielandshuis van Jacob Lois
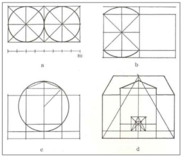
Hij begint met twee tegen elkaar geplaatste vierkanten, waardoor een rechthoek ontstaat van 80 x 40 voet. De cirkels die hij tekende waren een hulpmiddel om deze vierkanten perfect te construeren. In de tweede stap wordt de wortelverhouding aan de linkerkant getekend, waardoor er de zolderhoogte ontstaat. De diepte van de kelder eronder wordt gevonden met dezelfde wortelverhouding. In de derde stap wordt het centrale punt uitgewerkt. Hierdoor ontstaat een gevelritme van 20 - 40 - 20. De cirkel rond het centrale vierkant wordt enkel gebruikt om de hoogte van het fronton te vinden. Als laatste stap wordt de hoogte van het dak bepaald, door een gelijkzijdige driehoek te construeren. De centrale driehoek is verwezenlijkt volgens een proportioneel systeem dat in 1545 is gepubliceerd door Sebastiano Serlio. Ook de plattegrond van het Schielandshuis is ontworpen volgens een systeem. De plattegrond is een vierkant van 25 x 25 meter. De indeling van de binnenruimtes komt niet overeen met de gevel; terwijl de gevel is verdeeld in een ritme van 20 - 40 - 20, is de plattegrond verdeeld in drie traveeën in een ritme van 25 - 30 - 25. De plattegrondtekeningen vertonen per ruimte verschillende proportionele systemen. In de grote aula in het midden overlappen twee cirkels, die aangeven dat het een verhouding heeft van 2:3. Een kleinere kamer, aan de linkerkant, heeft echter een verhouding van 4:5.
Uit deze studie blijk dat dit waarschijnlijk de enige voorbeelden zijn van dergelijke geometrische systemen op basis van kruisende cirkels die in binnenruimten zijn getekend. Er is nauwelijks een geheel getal te vinden met een proportionele relatie tot het grid, aangezien de binnenmaten van de kamers veelal het resultaat waren van het grid minus de diktes van de wanden (en niet de uitgangspunten van een proportionele indeling). Maar, in dit bouwontwerp lijkt het erop dat Lois de dingen mooier presenteert dan dat ze eigenlijk waren, waarschijnlijk omdat hij kennis wou maken met de ideeën van Palladio en Scamozzi. De grote kamer aan de linkerkant is gemarkeerd met twee kruisende cirkels, wat dus suggereert dat deze ruimte een verhouding heeft van 2:3. Dit past echter niet goed in de kamer, omdat het niet op één lijn ligt met de achterwand, maar met een punt vlak voor de schoorsteen.
Door zulke studies worden algemene principes onthuld van de methode van wiskundig ontwerpen in de zeventiende-eeuw in Nederland. Er moet ten eerste een algemene omtrek van het volume of van de gevel worden gevonden. Dit moet bij voorkeur op basis gebeuren van een rechthoek die geconstrueerd is door vierkanten bij elkaar op te tellen. Deze rechthoek kan worden vergroot door volumes die zijn afgeleid van vierkantswortelverhoudingen. Zodra de hoofdlijnen zijn gedefinieerd, kunnen de klassieke proporties orden toegevoegd. Hierna kunnen de ornamenten worden toegevoegd. Om de plattegrond te ordenen wordt een grid gebruikt. Soms heeft dit te maken met de geven, maar soms ook niet. De wanden zijn getekend langs de lijnen van het grid, maar vanwege de wanddiktes is het resultaat dat de werkelijke binnenruimten nooit zo perfect kunnen zijn als het theoretisch aangegeven door het grid. Deze principes kunnen als uitgangspunt gebruikt worden, om zo andere ontwerpen uit dezelfde periode te onderzoeken.
Na de Renaissance
Met de opkomst van de nieuwe natuurwetenschap begon het wereldbeeld dat de micro- en macrokosmos bij elkaar had gehouden uiteen te vallen en was het snel gedaan met de alomvattende ordening en harmonie waarin de denkers vanaf de dagen van Pythagoras tot de zestiende en zeventiende eeuw hadden geloofd. Dit proces van 'atomisering' leidde uiteraard ook tot veranderingen op het gebied van de proportieleer.
De tijdsgeest na de Renaissance
Claude Perrault
In tegenstelling tot wat tot dan toe als algemeen wordt aangenomen, beweert Claude Perrault (1618 - 1688) dat er geen vast proportiesysteem bestaat. Hij zegt dat de proporties afhangen van de ontwerper, en dat proporties die 'de regel van de bouwkunst' volgen enkel aangenaam zijn omdat we eraan gewend zijn. Hij zegt dat niemand een overeenkomst kan vinden tussen twee gebouwen omdat niemand dezelfde regels heeft gevolgd, want men vindt in geen enkel traktaat hetzelfde, terwijl ze allemaal beweren gebaseerd te zijn op de Oudheid. Maar, het ontkennen van een vast proportiesysteem betekent ook het ondermijnen van drie vaste veronderstellingen die daarmee gepaard gaan; de analogie tussen architectuur en de harmonie in de muziek, de invloed die de verhoudingen van de natuur op de verhoudingen bij het ontstaan van de architectuur hadden uitgeoefend en de imitatie van de Oudheid. Bij gevolg verdedigt hij de relativiteit van ons esthetisch oordeel, en stelt dat muzikale consonanties niet in visuele proporties kunnen worden vertaald.
Perrault beweert dat schoonheid niet afhankelijk is van proporties en hij onderscheidt twee vormen van schoonheid, namelijk objectieve schoonheid en arbitraire schoonheid. Objectieve schoonheid wordt door iedereen als mooi ervaren; men herkent dit onmiddellijk en men wordt erdoor beroerd zoals bijvoorbeeld de grootte en de rijkheid van materialen. Arbitraire schoonheid hangt af van gewoonte, het is geen vrije of subjectieve schoonheid maar het is afhankelijk van het volk; de klasse op een bepaalde plaats of bepaalde tijd. Wat betreft ordegedachtes onderscheidt Perrault twee methodes. Bij de eerste methode verzamelen architecten de meest gewaardeerde voorbeelden uit oude en moderne werken, plaatsen deze naast elkaar zonder hier verder conclusies uit te trekken. De andere methode impliceert dat men een oordeel gaat vellen aan de hand van meningen van mensen met autoriteit. Zelf stelt hij een derde methode voor, het systeem van de Ouden. Dit is een eenvoudig verhoudingssysteem waarbinnen afwijkingen mogelijk zijn. Deze proporties zouden zo gekozen worden zodat ze makkelijk onder te verdelen en te onthouden zijn. Een latere analyse van Perraults voorstellen lijkt er op te wijzen dat hij koos voor een middenweg tussen de extreme gevallen die te vinden zijn in de geschiedenis.
De Moderniteit
De twee besproken proportiestelsels in de Europese kunst, het geometrische en het metrische, komen beide voort uit pythagoreïsche-platonische traditie. In de achttiende eeuw raakten deze echter in verval. Tot dan toe had niemand er ooit aan getwijfeld dat objectieve proportiemaatstaven een wezenlijk vereiste vormen voor elk kunstwerk. De 'nieuwe tijd' zou hier een verandering aan brengen.
Andere voorbeelden van een hernieuwd zoeken naar orde vallen buiten het domein van kunst. In uiteenlopende disciplines als filosofie, fysica, natuurwetenschap, wiskunde en psychologie wordt hetzelfde fundamentele probleem vanuit verschillende invalshoeken benaderd. Zo onderzoeken fysiologen bijvoorbeeld hoe zintuigprikkels in de hersenen worden geordend; de psychologen het ordenend vermogen van de hersenen; biologen, histologen en kristallograven de geometrie van dieren, planeten en kristallen. Tegelijkertijd grijpen wiskundigen, zoals Einstein, terug op het wezenlijk platonische begrip van een vooraf bepaalde harmonie.
De tijdsgeest van de Moderniteit
De negentiende-eeuwse opvatting was dat de kunstenaar volledig op zijn intuïtie af moest gaan om orde in de chaos te scheppen. Schoonheid en proportie werden in de nieuwe tijd opgevat als psychologische verschijnselen, voortkomend uit en inherent aan de geest van de kunstenaar. Voortaan werden schoonheid en proportie toegeschreven aan een irrationeel opgevatte creatieve drift.
Dit was de reactie van de kunstenaar op het nieuwe wereldbeeld dat vanaf de zeventiende eeuw zijn intrede deed: een universum, beheerst door de wetten der mechanica en ijzeren noodzaak, zonder verborgen plan, waar, in tegenstelling met alle eerdere beschavingen en voor het eerst in de geschiedenis, de mens zijn unieke en geprivilegieerde plaats was kwijtgeraakt. In de hele geschiedenis (althans van de hogere beschavingen) had zich nog nooit de situatie voorgedaan dat de keuze van een ordeningssysteem volledig aan de individuele kunstenaar werd overgelaten.
Andere voorbeelden van een hernieuwd zoeken naar orde vallen buiten het domein van kunst. In uiteenlopende disciplines als filosofie, fysica, natuurwetenschap, wiskunde en psychologie wordt hetzelfde fundamentele probleem vanuit verschillende invalshoeken benaderd. Zo onderzoeken fysiologen bijvoorbeeld hoe zintuigprikkels in de hersenen worden geordend; de psychologen het ordenend vermogen van de hersenen; biologen, histologen en kristallograven de geometrie van dieren, planeten en kristallen. Tegelijkertijd grijpen wiskundigen, zoals Einstein, terug op het wezenlijk platonische begrip van een vooraf bepaalde harmonie.
Kubisme
De eerste kentering in de artistieke benadering van de proportie deed zich in feite al in het eerste decennium van de vorige eeuw voor in het werk van de kubisten, die de conventionele schema’s overboord zetten en wilden terugkeren naar elementaire geometrische vormen.
Modulor-schaal
Le Corbusier kwam met het principe van de Modulor schaal. Met deze benadering ging hij niet uit van universele beginselen - maar van de mens. Op deze manier gaf hij ook weer dat er een verschuiving plaatsvond, van absolute naar relatieve maatstaven. Oudere proportiestelsels kwamen voort uit de systematische ontwikkeling van een geometrisch grondprincipe, de Modulor is anders van opzet. De basiselementen ervan zijn uiterst simpel: het vierkant en het dubbele vierkant. Deze geometrische basisvormen worden gecombineerd met twee verschillende reeksen getallen op basis van de gulden snede.
Tegelijkertijd getuigt de Modular van de sterke samenhang van ons culturele erfgoed. Net als de proporties van de Middeleeuwen, en de aritmische muzikale proporties van de Renaissance, is Le Corbusiers systeem ook een bijdrage aan inzichten die het pythagoreïsch-platonische denken voor de westerling ontsloot.