Berekening van Constructies/Deel 1, pagina 10

Deel 1, pagina 10

Deel 1, pagina 10

Tekst (OCR)

Deze uitkomst kan als volgt worden verwoord:

De doorbuiging in een punt U ten opzichte van de raaklijn in een ander punt A van de elastische lijn is gelijk aan het statisch moment om U_van het deel van het gereduceerde-momentenvlak begrepen tussen A en U (en gearceerd in fig. 9.b).

2.2.1.5. De bovenstaande vier eigenschappen van het gereduceerde-momentenvlak kunnen ook op andere manieren worden bewezen. Ze zijn bijzonder handig bij de berekening van elastische ver- plaatsingen en draaiingen voor liggers. De regels 2.2.1.1 en 2.2.1.2 worden soms de analogieén van Mour en de regels 2.2.1.3 en 2.2.1.4 de stellingen van GREENE genoemd.

2.2.1.6. VOORBEELDEN

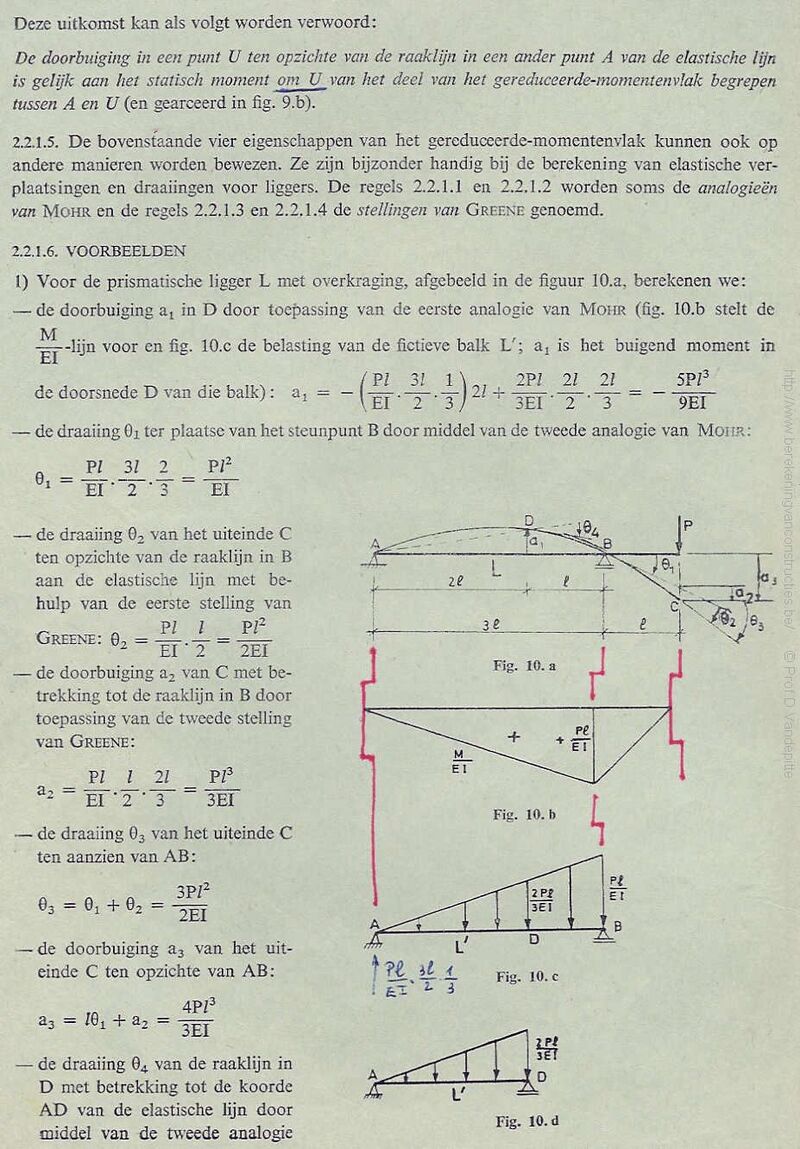
1) Voor de prismatische ligger L met overkraging, afgebeeld in de figuur 10.a, berekenen we:

— de doorbuiging a, in D door toepassing van de eerste analogie van Mour (fig. 10.b stelt de

¥ tin voor en fig. 10.c de belasting van de fictieve balk L’; a, is het buigend moment in

3 3 a 31 y)2+ 2p 2) 2h SP

de doorsnede D van die balk): a, = HS =

S51 Se US — de draaiing 0; ter plaatse van het steunpunt B door middel van de tweede analogie van Morir:

i stl ide Bie 2es5 EL

— de draaiing 0, van het uiteinde C ten opzichte van de raaklijn in B aan de elastis lijn met be- hulp van de eerste stelling van

ae GREENE: 0, = =r°> = DED

— de doorbuiging a, van C met be- trekking tot de raaklijn in B door toepassing van de tweede stelling van GREENE:

7 Sebi 2 3a) SEE — de draaiing 0; yan het uiteinde C ten aanzien van AB:

3Pi?

0; = 0:40 = +

—de doorbuiging a; van het uit- einde C ten opzichte van AB:

4pr°

a; = 10; + a2 = 35P

— de draaiing 6, van de raaklijn in D met betrekking tot de koorde AD van de elastische lijn door middel van de tweede analogie

Wy =